Einstein’s Masterpiece

Our understanding of the physical world was shaped decisively by two scientific revolutions in the early twentieth century — and Albert Einstein had a hand in each. But whereas one, quantum mechanics, was the work of many scientists, the other, relativity, we owe almost entirely to Einstein’s singular mind. The theory of special relativity that Einstein introduced in 1905 while working as a technical assistant in the Swiss patent office reconfigured our basic notions of space and time. It eventually led to the more comprehensive general theory of relativity ten years later. Together, the theories upended centuries of physics and laid the groundwork for modern cosmology. Who knows if there will ever be another single scientist to demonstrate so rigorously, through thought experiments, mathematical arguments, and bold empirical predictions, that our universe is vastly more strange and wondrous than it ever appeared to common sense or to earlier generations of scientists.

It has now been a century since Einstein introduced his general theory of relativity in a series of lectures in November 1915. The theory, which connects space and time with matter, energy, and gravitation, has since helped scientists discover black holes, extrapolate the properties of the universe backwards in time to the Big Bang, and come tantalizingly close to glimpsing traces of gravitational waves reverberating from the earliest moments of the universe.

General relativity has served as a paragon of a scientific theory, and generations of physicists have hailed its sublimity. Ernest Rutherford, for instance: “the theory of relativity by Einstein … cannot but be regarded as a magnificent work of art.” Wolfgang Pauli: “it will always remain the pattern of a theory of consummate beauty of the mathematical structure.” Sean Carroll: “General relativity is the most beautiful physical theory ever invented.” One hundred years, and a theory that sprung from Einstein’s capacious imagination still withstands ever-finer empirical tests, still guides physicists trying to discern basic features of our universe.

And yet, for Einstein, the theory was “only an outlying ridge in the arduous climb to a greater goal that he never achieved,” as physicist John Archibald Wheeler described it. Einstein’s greater goal, which some physicists came to see as quixotic, was to combine gravitation and electromagnetism into a single theory — a “unified field theory” — that would also resolve some conceptual issues with quantum mechanics that still perplex us today. Even though Einstein, like all physicists who have followed in his path, never succeeded in this quest to fully unify the basic physical forces, the general theory of relativity still astonishes and inspires all who behold it; in Wheeler’s words, it left us “with an ideal for a physical theory that has never been surpassed.” The centennial provides a fitting occasion to examine, with the help of several excellent new books, how and why general relativity came to be.

Before turning to Einstein’s quest for general relativity, it will be helpful to provide a bit of background on the theory and describe some of its basic concepts. In 1905, during his annus mirabilis, Einstein introduced what came to be called the special theory of relativity. As he presented it, the theory starts from only two postulates, both of which were supported by significant experimental evidence. The first, which Einstein labeled the principle or postulate of relativity, states that “the same laws of electrodynamics and optics will be valid for all frames of reference for which the equations of mechanics hold good.” A frame of reference is basically a coordinate system for measuring the motions of objects. An easy way to understand the idea is to consider the following example. A sea captain walking toward the bow of his ship while the ship is sailing at a fixed speed moves relative to the ship (his reference frame). But to somebody watching from shore, the ship (with its captain) moves relative to the shore (the onlooker’s reference frame). Both the onlooker and the captain experience the same laws of motion in their respective reference frames.

The reference frames Einstein was concerned with are called inertial reference frames. While their definition can get fairly tricky, they are roughly the frames corresponding with objects in non-accelerated — or straight and uniform — motion. (In the example of the ship, both reference frames are inertial reference frames.) Now, classical physicists understood that the laws of motion are the same in all inertial reference frames — a principle known as Galilean relativity. It was less clear, however, if this relativity principle extended to electromagnetic and optical phenomena, but Einstein thought that the experimental evidence suggested it did. Hence Einstein’s innovation was not to discover the principle of relativity but to extend it in a novel way and to draw from it some very important and surprising consequences. (His theory came to be called the special theory of relativity later, when Einstein sought to come up with a general version that would extend the relativity principle to all frames of reference.)

Einstein’s second postulate, sometimes called the light postulate, drew from nineteenth-century electromagnetic theory. It states that “light is always propagated in empty space with a definite velocity c which is independent of the state of motion of the emitting body,” as measured from any inertial frame of reference. The problem was how to reconcile the two postulates. Consider two observers who are in non-accelerated motion with respect to each other. If one observer, Sarah, stands on a train platform, while another observer, Joe, sits in a train traveling east at 50 miles per hour, they will measure the velocity of a second train moving westward differently. Let’s say that the westward train moves toward Sarah and the platform — her frame of reference — at 100 miles an hour. According to classical mechanics, Joe will perceive the train to be moving toward his train — his frame of reference — at 150 miles per hour. So far, so classical. But now consider how they will each measure a beam of light traveling westward: it might seem that the beam of light should be moving, like the westbound train, 50 miles per hour faster for Joe than for Sarah. According to Einstein’s light postulate, however, the light beam must move at the same velocity for both of them. Even if Joe were moving toward (or away) from the source of the light at half the speed of light, according to the postulate, his measurements of the light’s velocity will be exactly the same as Sarah’s. This seems baffling: how can something have the same velocity as measured by observers who are in motion relative to each other?

Einstein’s genius was to demonstrate that his two postulates could be harmonized by radically revising classical notions of space and time. He solved the problem by rethinking the very concept of simultaneity: observers who are moving uniformly with respect to each other will obtain the same measurements for the speed of light, but they will disagree about whether or not events take place at the same time. This disagreement is problematic only if we assume that time is absolute — an assumption built into physics since the days of Newton. But if, as Einstein postulated, the speed of light is the same for all observers in inertial reference frames, then something else has to give. In reconciling the principle of relativity with the light postulate, Einstein did away with the long-held idea that there could be absolutely simultaneous events.

A few years later, Hermann Minkowski, a former teacher of Einstein’s at ETH Zurich who remembered his student as “a lazy dog,” greatly clarified the theory by showing that it could best be understood within a specific type of four-dimensional geometry. The modern concept of spacetime was born. The concept itself is fairly simple: a coordinate system in which all events are specified by their positions in three dimensions of space and one dimension of time. Minkowski’s geometrical formulation would prove indispensable in Einstein’s quest for general relativity. As we will see, general relativity posits a much stranger and more dynamic geometry for spacetime. In many ways the transition from special to general relativity is more radical even than the transition from nineteenth-century physics to special relativity.

Readers who want to trace Einstein’s winding path toward the general theory can learn from an excellent new book, The Road to Relativity, by Hanoch Gutfreund and Jürgen Renn. Gutfreund, a physicist, is an academic director of the Albert Einstein Archives at Hebrew University in Jerusalem; Renn, a historian of science who directs the Max Planck Institute for the History of Science in Berlin, has published extensively on Einstein. The Road to Relativity contains a facsimile of Einstein’s 1916 manuscript, “Die Grundlage der allgemeinen Relativitätstheorie” (along with its English translation as “The Foundation of the General Theory of Relativity”), his first attempt to present the theory in writing in a clear and comprehensive manner. Gutfreund and Renn also offer a rich page-by-page commentary on the text, explaining Einstein’s thinking and providing important background information for understanding the progression of Einstein’s ideas. They also give a lucid and dramatic account of Einstein’s “intellectual odyssey” toward general relativity from 1907–1915. Their account draws especially on the past two decades of historical research on this topic.

The Road to Relativity should interest anyone — including readers with no exposure to college-level physics — who can sympathize with what Einstein described as “the years of searching in the dark for a truth that one feels, but cannot express; the intense desire and the alternations of confidence and misgiving, until one breaks through to clarity and understanding.” Gutfreund and Renn have also edited an anniversary edition of Einstein’s 1917 book Relativity: The Special and the General Theory, which Einstein wrote to explain the theories to a popular audience.

One refreshing quality of these two volumes is how they reveal not only Einstein’s methods, but also the man himself. The image of Einstein that prevails in our culture often threatens to obscure the limits to his own abilities and the great difficulties he faced in developing his theory. If “genius” signifies someone whose intellectual and creative capacities far outstrip those of peers, and whose best work seems comparatively effortless, then, as The Road to Relativity illustrates quite well, Einstein was at best a faltering genius. While he did much of his work independently, he relied on the contributions of people such as Marcel Grossmann, who coauthored an early version of general relativity (called the Entwurf version, from the German for “draft”), and introduced Einstein to a mathematical method called tensor calculus that is essential for many of the theory’s calculations. Someone who played a similar role was Michele Besso, who warned Einstein about a flaw in the Entwurf equations and helped him with early calculations of the predicted orbit of Mercury. And, as Gutfreund and Renn show, Einstein struggled mightily to find his way to the light. In 1912, he wrote to a colleague, “one thing is certain: never before in my life have I toiled any where near as much.” Einstein’s genius lay not principally in his great talent for mathematics and physics, but in his great creativity and sheer determination to carry on toward a summit he perceived sometimes dimly.

Since special relativity established a new understanding of space and time, “all physical interactions needed henceforth to fit within its framework,” as Gutfreund and Renn put it. This work of reconciling old theories with the new conception took several years. Electromagnetism did not present a serious obstacle to Einstein’s special relativity; indeed, special relativity was partly formulated in response to difficulties stemming from Maxwell’s theory of electromagnetism. Gravity, too, seemed as though it could be reconciled with special relativity somewhat easily. Gravity was problematic for the new theory because Newton’s law of gravitation assumes instantaneous action at a distance, whereas in special relativity there are no physical effects that can propagate faster than the speed of light, and there is no notion of absolute simultaneity. But many theories were developed between 1905 and 1915, including by Hermann Minkowski and Henri Poincaré, that managed to overcome these apparent difficulties. As John D. Norton writes in an excellent article on the subject, “the problem was not whether [reconciling Newtonian gravitation with special relativity] could be done, but how to choose the best of the many possibilities perceived, given the expectation that relativistic corrections to Newtonian theory might not have measurable consequences even in the very sensitive domain of planetary astronomy.”

Since these other theories were already taking shape, why did Einstein choose to pursue his own, more revolutionary theory? The answer is not that he thought the various attempts at reconciling gravity and special relativity would fail to produce accurate empirical predictions. Rather, attempts made along these lines, Einstein wrote, “clearly failed to do justice to the most fundamental property of gravitation” — that all objects fall with the same acceleration, regardless of their mass or type of matter.

In Newtonian mechanics, this property manifests itself in the equivalence of inertial mass (which determines an object’s resistance to acceleration) and gravitational mass (which determines the force with which an object is attracted to other bodies). Objects with greater mass are attracted to one another with greater gravitational force, but have a proportionally greater inertial resistance to acceleration, so the acceleration caused by gravity ends up being the same. Einstein realized that this curious fact suggested a deeper connection between inertia and gravity than Newtonian physics could offer; as he later wrote, “I was in the highest degree amazed at its existence and guessed that in it must lie the key to a deeper understanding of inertia and gravitation.” Einstein concluded that attempts to incorporate gravitation into special relativity require forgoing the equivalence of gravitational and inertial mass (and thus the principle that all objects fall with the same acceleration), even though the difference would likely be too small to detect through experiment.

Einstein was also troubled by what he saw as a deficiency in his special theory of relativity. Like classical mechanics, special relativity identifies a special set of reference frames for the description of physical processes — inertial reference frames. But why would the principle of relativity not apply to both inertial and non-inertial frames of reference, such as rotating or accelerating reference frames. And why should there be a strict distinction between these frames? Einstein, ever seeking after deeper explanations, was bothered by these seemingly brute facts of classical mechanics and special relativity. In his book Relativity he likens it to standing in front of a stove with two pots of water, one emitting steam and the other not, and becoming “astonished and dissatisfied” upon finding no cause for the difference between the two pots. Einstein’s intuition, put in terms of this analogy, was that the two pots might not actually be different. “Is it conceivable,” he asked in a 1907 review article, “that the principle of relativity holds also for systems which are accelerated with respect to each other?” He would later describe the preferred status of inertial reference frames in special relativity as an “inherent epistemological defect.”

While writing the 1907 review article, Einstein had what he later referred to as the “happiest thought of my life,” which he quickly felt was the way to extend the principle of relativity to accelerated motion. The thought, as Einstein put it years later, was that “ … the gravitational field only has a relative existence. Because, for an observer freely falling from the roof of a house, no gravitational field exists while he is falling, at least not in his immediate surroundings” (emphasis in the original). This was a very powerful thought, which Einstein developed into what he called the “principle of equivalence.” The principle implies that any experiment carried out while freely falling in a uniform gravitational field will give the same result as when carried out in a non-accelerating frame of reference in empty space. Similarly, any experiment performed in a uniformly accelerated frame of reference will have the same result when performed while at rest in a uniform gravitational field. To summarize, “gravitation and acceleration are to some extent interchangeable,” as Gutfreund and Renn put it.

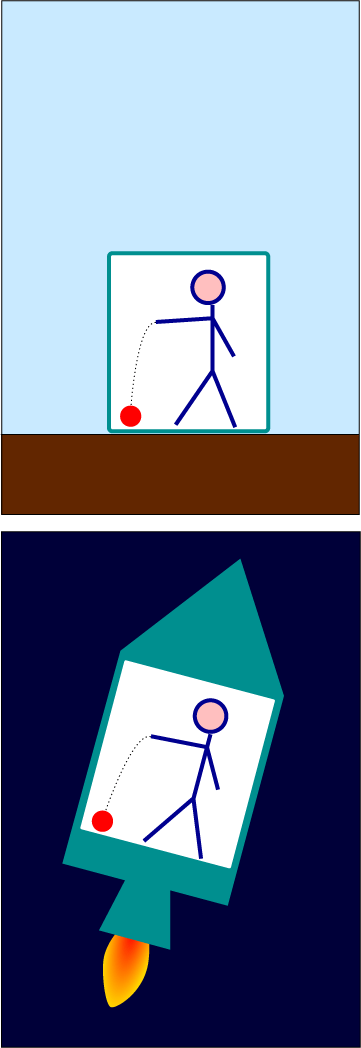
To illustrate the idea, imagine you are standing in an elevator without windows. You let an object fall out of your hands and drop to the floor of the elevator (as in the top image to the right). The object falls with an acceleration of 9.8 meters per second squared — precisely the acceleration at which objects fall to earth when under the influence of gravity. Should you therefore conclude that the elevator is sitting on the surface of the earth? How do you know the elevator is not in outer space — far away from any gravitational influence — accelerating “upward” at exactly 9.8 meters per second squared (as in the bottom image to the right)? There is no observable difference; no experiment performed inside the elevator can settle the matter (if we assume, for simplicity, that Earth’s gravitational field is perfectly uniform). The phenomena in both elevators are for all intents and purposes empirically equivalent.

Einstein still had a long way to go in formulating the theory, but he had made a conceptual breakthrough. The equivalence principle suggested to Einstein that the motion of an object in a gravitational field is not caused by any force, but rather results from a curvature in spacetime itself. The difference can be illustrated by the following example. According to the older Newtonian understanding, a cannonball falling freely toward the ground is subjected to a gravitational force that pulls the cannonball downward, causing it to accelerate. By contrast, according to Einstein’s equivalence principle, the cannonball is not subject to any force at all — “If a person falls freely, he will not feel his own weight.” What, if not a force, can account for the apparent acceleration of the cannonball as it falls? Einstein’s insight was that it was the curvature of spacetime caused by the mass of the Earth. The equivalence principle also suggests that the curvature of spacetime will be dependent on the sources of gravitational fields. But perhaps most importantly, it leads to a new understanding of gravitation: as Gutfreund and Renn describe it, “the gravitational field was no longer considered to be a force in the sense of Newtonian physics but as the embodiment of geometric properties of a generalized spacetime continuum.”

The principle of equivalence has some striking empirical consequences. For example, it implies the bending of light in gravitational fields, a prediction that was famously confirmed by Arthur Eddington’s observations of stars near the sun during a solar eclipse in 1919. The sun’s gravitational field makes the light rays from faraway stars appear to bend as they pass around the sun. In fact, the light does not actually bend. What happens, according to Einstein, is that the mass of the sun causes the surrounding spacetime to warp. So when light rays pass around the sun, they appear to bend toward it. A special kind of geometry was ultimately required to describe this complex spacetime effect.

Indeed, one of Einstein’s major challenges over the next several years was finding the correct mathematical formulations for his theory. He was convinced that he was heading in the right direction, even when other leading physicists expressed skepticism. Max Planck, who helped launch the quantum revolution and was one of the first physicists to recognize the brilliance of Einstein’s 1905 work, reportedly told Einstein in 1913: “As an older friend I must advise you against it for in the first place you will not succeed; and even if you succeed, no one will believe you.” But Einstein was determined. Abraham Pais, in his wonderful scientific biography of Einstein, Subtle is the Lord (1982), writes:

Others might have shied away from the equivalence principle in order to retain the global invariance. Not so Einstein. With a total lack of fear he starts on the new road. For the next eight years he has no choice. He has to go on. From then on also his style changes. If the work of 1905 has the quality of Mozart, then the work of 1907–15 is reminiscent of Beethoven. The quotation at the head of this chapter is the motto of the last movement of Beethoven’s opus 135: Must it be? It must be.

Einstein’s primary struggle during this period was to derive an equation, or a set of equations, describing how matter and energy influence the geometry of spacetime. (It is this equation — rather than the far more famous E=mc², a fairly straightforward consequence of special relativity — that deserves to be remembered as Einstein’s most revolutionary equation.) Known as the field equation, it had to satisfy a number of constraints, such as reproducing the results of Newton’s law of gravitation under normal circumstances (a condition known as the Newtonian limit), and not violating the conservation of energy. It had to satisfy Einstein’s own equivalence principle. And it had to be generally covariant. (General covariance is a property of equations for physical laws; if the equations are generally covariant, they will have the same form under arbitrary transformations of coordinate systems.) Between 1912 and 1915, Einstein labored to derive an equation satisfying all these requirements through two complementary strategies: a physical strategy, starting with an equation that satisfied the Newtonian limit and checking if it had the right covariance, and a mathematical strategy, starting with covariant equations and trying to modify them to satisfy the physical requirements. Although he had come a long way, by September 1915 he realized that he had spent years trekking down the wrong path.

Late that month, Einstein wrote a letter to Erwin Freundlich, the first German astronomer to take his gravitational ideas seriously. In a tone bordering on despair, Einstein explained that he had discovered a logical contradiction in the theory of gravitation that he was developing:

Either the equations are numerically incorrect (number coefficients) or I apply the equations in a fundamentally wrong way. I do not believe I am able to find the mistake myself, for in this matter my mind is too set in a deep rut. More likely, I have to rely on some fellow human being with unspoiled brain matter finding the mistake. Don’t forget to spend some time on the matter when you can. Best wishes, your A. Einstein.

In the letter, Einstein also concludes that his theory could not solve a longstanding problem in astronomy: a century of observations had shown that Mercury did not orbit the sun exactly as predicted by Newton’s equations. A correct theory of gravitation would have to account for this discrepancy — the so-called precession of the perihelion of Mercury — something that Einstein had recognized by 1907. The rut that Einstein had settled into by September 1915, then, threatened to keep him from realizing some of his main hopes for a relativistic theory of gravitation.

In fact, Einstein had been close to a solution in 1912, but had erroneously judged along with his collaborator Marcel Grossman that their equations could not satisfy all the requirements. In particular, he thought their equations could either satisfy the physical requirements (the Newtonian limit and the conservation of energy) or the mathematical requirement of general covariance, not both. Einstein decided to preserve the physical requirements — thus forgoing general covariance — in order to reproduce Newton’s law of gravitation under normal circumstances. This decision, which represented a temporary triumph of the physical approach and which led to the equations of the Entwurf theory, would haunt him over the next few years.

Shortly after Einstein reached his point of despair in late September 1915, he found a way forward by returning to the equations that he and Grossman had previously set aside. He now saw that the mathematical approach might in fact offer a route to the correct theory. In an astonishing flurry of work, during which he was competing against David Hilbert, one of the greatest mathematicians of the twentieth century, to derive the correct equations, Einstein submitted four papers to the Royal Prussian Academy of Sciences in November 1915, which he also presented as lectures. In the first of these papers, entitled “On the General Theory of Relativity,” Einstein explained how he returned to general covariance, a “demand from which I parted, though with a heavy heart, three years ago when I worked together with my friend Grossman.” The second paper, which Einstein submitted as an addendum to the first, resolved a few questions that the first had left unanswered. In the third paper, Einstein used his new theory to calculate the predicted orbit of Mercury, and found that it corresponded exactly with the observations. As he would later put it in a letter:

Imagine my joy at the recognition of the feasibility of general covariance and at the result that the equations correctly yield the perihelion motion of Mercury. I was beside myself for several days in joyous excitement.

And then, on November 25, 1915, Einstein presented the final paper to the Prussian Academy, completing the theory of general relativity by making a small modification to the findings of the first two papers. In under two months, Einstein had found his way to a theory that satisfied all the mathematical and physical requirements, discovered that it correctly predicted the orbit of Mercury, and, he felt, succeeded in generalizing the principle of relativity from 1905. (Many scholars have argued that Einstein was less successful in meeting this goal than he thought.) Einstein called this time “one of the most exciting and strenuous” of his life, a period in which his “wildest dreams have been fulfilled.”

What exactly Einstein had accomplished was not immediately clear. Jürgen Neffe claims in his 2007 biography of Einstein that the audience at the Prussian Academy “did not know what to make” of Einstein’s theory. Einstein wrote the day after his fourth and final lecture that “only one colleague has really understood it” (his emphasis). That colleague was David Hilbert, and Einstein felt that Hilbert had been trying to appropriate some of his results without acknowledgment. It certainly did not help for the reception of the theory that Europe was collapsing under the weight of the First World War. Gutfreund and Renn say that none of Einstein’s famous colleagues in Berlin devoted serious attention to his theory at first, and note that he struggled to convince astronomers to test his theory’s prediction that gravity deflects light.

But Einstein was well aware of the revolutionary nature of what he had found. Like the special theory before it, the general theory of relativity postulates that physical processes unfold in a four-dimensional spacetime continuum. But according to general relativity, spacetime itself is curved: the geometry of spacetime is such that straight lines can intersect more than once. Even more revolutionary, the theory requires that the curvature of spacetime vary, like a surface with peaks and valleys and undulations, depending on the distribution of matter and energy. As John Stachel puts it in the foreword to The Road to Relativity, “space-time structures no longer form a fixed stage, on which different dramas of matter and fields may be enacted: stage and actors interact. A new drama requires a new stage.” The very structure of spacetime is dynamic, like the physical processes that unfold within it.

David Hilbert, referring to the mathematical institute he had helped create at the University of Göttingen, supposedly said that “every boy in the streets of our mathematical Göttingen understands more about four-dimensional geometry than Einstein. Yet, despite that, Einstein did the work and not the mathematicians.” Why was it Einstein who led the way to general relativity, and not other leading physicists (such as Poincaré and Hendrik Lorentz) who had more experience and possibly greater mathematical abilities? John Archibald Wheeler has suggested that Einstein’s time at the patent office gave him a unique ability to discern patterns amid confusion: “Who else could have distilled this simple central point from all the clutter of electromagnetism than someone whose job it was over and over each day to extract simplicity out of complexity?” Einstein seems to have had an abiding faith in the methodological power of simplicity, which would become more visible during his later efforts to find a unified field theory.

Einstein’s faith in simplicity was philosophically nuanced and was informed by his successes. In the latter half of his life, he often wrote of the value of simplicity and unification in scientific theorizing, as in a 1942 letter to a physicist friend: “You are the only person known to me who holds the same orientation to physics as I: belief in the comprehensibility of reality through something logically simple and unified…. It appears difficult to peek into the cards of the Lord God.” In a 1950 Scientific American article, Einstein asked, “What, then, impels us to devise theory after theory? Why do we devise theories at all?” The answer, he wrote, is that we are motivated to strive “toward unification and simplification of the premises of the theory as a whole.”

What grounded Einstein’s faith in the value of simplicity was no mere aesthetic preference nor a pragmatic concern for devising useful theories. He came to view simplicity as a powerful guide when experimental results alone could not illuminate the path to the correct theory. Mathematical simplicity in particular became decisive for Einstein, as he was, in his own words, “made, by the problem of gravitation, into a believing rationalist, that is, into someone who seeks the only trustworthy source of truth in mathematical simplicity.” He later wrote that “The equations of gravitation were only found on the basis of a purely formal principle [general covariance], that is to say, on the basis of trust in the greatest logical simplicity of laws of nature thinkable.”

Even well before 1915, Einstein had demonstrated an ability to unify disparate phenomena under simple and general principles. Abraham Pais cites the very first sentence of Einstein’s 1905 special relativity paper (which states that Maxwell’s electrodynamics “leads to asymmetries which do not appear to be inherent in the phenomena”) to argue that Einstein was driven to the special theory of relativity by considerations of simplicity — a “magnificent obsession” that “was to lead him to his greatest achievement, general relativity, and to his noble failure, unified field theory.” Special relativity had resolved apparent contradictions in classical physics; general relativity had united special relativity and gravitation; and the unified field theory would, he hoped, do a similar thing for gravitation and electromagnetism. Whether or not Einstein’s obsession with simplicity helps explain why it was he and not others who discovered a fundamentally new theory of gravitation will have to await further reckoning. But Einstein’s ability to express an ultimately harmonious and comprehensible order behind natural phenomena distinguishes him from nearly all other physicists of his day.

The story of how Einstein’s theory came to be recognized, tested, and harnessed by the scientific community over the last century is fascinating in its own right. Readers unafraid of technical detail might enjoy General Relativity and Gravitation: A Centennial Perspective, which explores the discoveries that general relativity made possible. Edited by four physicists, the book consists of a dozen reviews of current research topics related to general relativity, covering such areas as inflationary cosmology, gravitational waves, and quantum gravity. The book is aimed at researchers, but its preface and introduction will be accessible to most readers, and one interesting chapter that provides a historical overview of general relativity is not too technical. The book also maps the current frontiers opened up by the theory in high-energy astrophysics and cosmology, some of which emerged quite recently.

Perhaps the most pressing and interesting questions raised by general relativity involve its relationship with quantum theory. One chapter in General Relativity and Gravitation reviews recent attempts to make headway on this problem. As early as 1916, it turns out, Einstein was aware of some ways that his general theory of relativity was incompatible with quantum mechanics. And general relativity, he knew, would not be the final word on gravitation. “The day will come,” he wrote in 1917 to the German mathematician Felix Klein, “when this way of conceiving [of gravitation] will have to give way to another that differs from it fundamentally, for reasons that today we cannot even imagine.”

Physicists and philosophers of physics have been working to imagine such reasons with special vigor in recent decades, though there remains a lack of consensus about where exactly the problems in reconciling the two theories lie. It is well-established, both theoretically and empirically, that particles governed by quantum laws can exhibit connections — they can “communicate” or display correlations — even when the particles are separated in spacetime at positions that cannot be traversed by light. Since special and general relativity are usually taken to prohibit signals from traveling faster than light, it seems that their accounts of spacetime structure will have to be modified to accommodate these startling quantum phenomena. However, there remains much disagreement about what exactly relativity prohibits from traveling faster than light: matter and energy seem clearly to be, but what about causal processes or information? Like many discoveries that have come out of quantum mechanics over the last century, these issues can be complex and difficult to fathom, and experts disagree about the best way of understanding them.

Besides this set of problems, there is another stemming from the fact that general relativity accounts for gravity in a “classical” manner, meaning that it treats physical quantities, such as position and velocity, as always having determinate values, unlike quantum mechanics, which treats these quantities probabilistically. Some physicists have tried to “quantize” the gravitational field, but have run into vexing technical and conceptual problems. There are also important empirical issues, such as the black hole firewall paradox, which suggests that Einstein’s equivalence principle or quantum field theory might be wrong.

Wolfgang Pauli wrote that “Einstein’s life ended with a question for physical science and a demand on us for synthesis.” One hundred years into the era of general relativity, that question and demand are as loud as ever.